Equilateral triangle
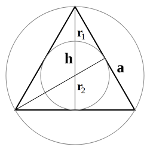
To the mobile versionThis is a calculator for lengths and the area of an equilateral triangle.. All sides have the same length and the angles measure 60° each. All altitudes, medians, angular bisectors, and side bisectors have the same length.
| Similar calculations | |||
|---|---|---|---|
| Square/Cube | Distances, areas, volume of a square and a cube | ||
| Regular hexagon | Distances and area | ||
| Rectangular triangle | Distances, angles, area in a rectangular triangle | ||
| Area 1 | Various area units (decimal partitioning) | ||
Usage: Type a known value of the triangle into the respective field. Click on any free space of the window or on the "calculate"-button and read the result. Use the "reset" button to delete your calculation. The units change in correspondance to the input values (cm and cm² or m and m² etc.).
Example: The segment bisector of an equilateral triangle is 10 cm long. What is the length of the triangle's sides? Since the segment bisectors and the altitudes have the same length, type "10" into the field for the height. Click on any free space of the window or on the "calculate"-button. Read the result for the side length (11.547 cm).
Remarks:
- Please note the remarks about the
representation of numbers..
- There is no warranty for the calculation. Cactus2000 is not
responsible for damage of any kind caused by wrong results.
- Please send an email if you have suggestions or if you would like to see more
conversions to be included.
© Bernd Krüger, 02.02.2020